現在のオーディオシステムの解決すべき問題点

こうして、理想的なスピーカーを探し求めるという事は、ジャズを聴くのに適した、ウッドベースの音をリアルでクリアに再生できるスピーカーを探し求める事となった訳です。

そこで、日本にあるあらゆるスピーカーを試聴致しました。しかし、残念ながら私の考えていたようなスピーカーにはなかなか巡り合いませんでした。

ならば、自分で開発するしかない、という事で改めて現在のマイクで音を録ってスピーカーで再生するオーディオシステムを再検討した結果、大変大きな問題が有る事に気が付いたのです。

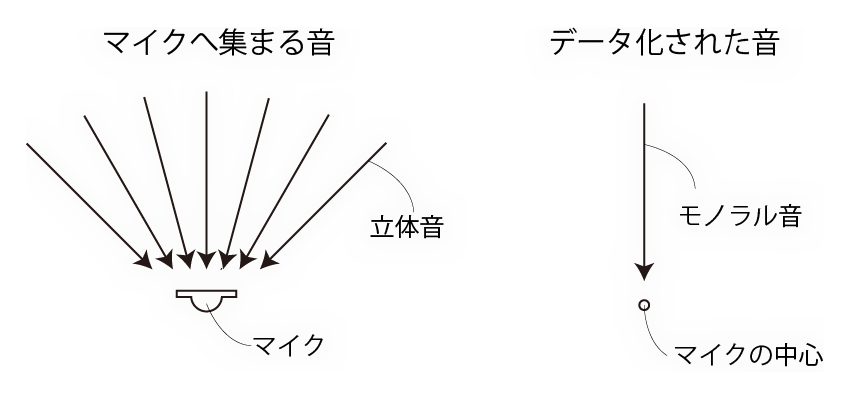
自然界に聞こえる音、楽器が出す音などの立体的に聞こえる音をマイクで録った音は、立体感のないモノラルの音としてデータ化されます。なぜならボイスコイルは前後方向の単一の方向にしか運動できないので、マイクの振動板が位相の違いにより複雑な運動をしたとしても、すなわちどこから音が来たのかの情報は無視されて、モノラルの音がマイクの中心の点へ来たと仮定して動作するからです。

多分多くの人は、「マイクはその場所の現実の音を拾ったんだから、その振動板が往復振動して得られた信号を忠実にスピーカーの振動板が往復運動して音を再生 出来る事こそが最も理想的なオーディオシステムだ」と思っているでしょうけれど、実はこのままでは少し問題が有ります。

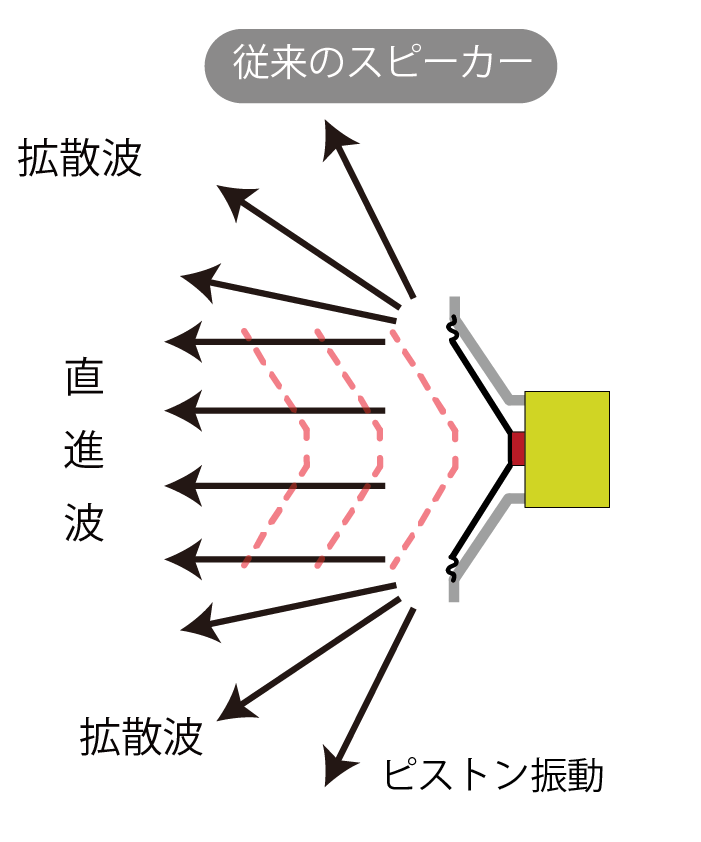
これをこのまま従来のスピーカーの振動板を平行往復運動＝ピストン運動させると、振動板の面積内からは振動板のコーンの形の直進波が出て、元のマイクがあった環境の再現にはなっていません。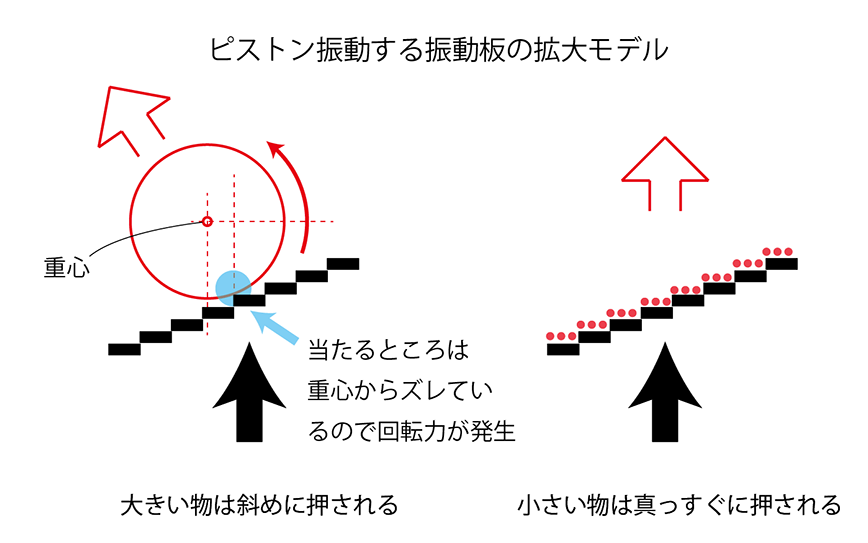

しかし、従来のスピーカー振動板の形状がコーン型に円錐形になっているので、振動板から直接に円錐に沿って斜め方向に出ると思われるでしょうが、それは違います。そのような事が起きるのは振動板の表面の分子より大きなものが動かされる場合です。

振動板の表面の分子に入り込んでいる空気は、振動板がピストン運動したら、そのピストン方向に動くしかありません。なぜなら既に紙分子の中に空気分子は入り込んでいるので横には動けないからです。この結果、従来のコーン型の振動板からはコーン型の面の直進波の音が出ることになります。

この問題を解決するためには、最初から拡散波の音を出せるスピーカーを模索する必要があります。

,

r

問題の解決策〜拡散波を出すスピーカーのススメ

まず、拡散波のモデルとして球面波にはどのような性質があるのかを詳しく再検討してみました。球面波を出すのは点音源とします。

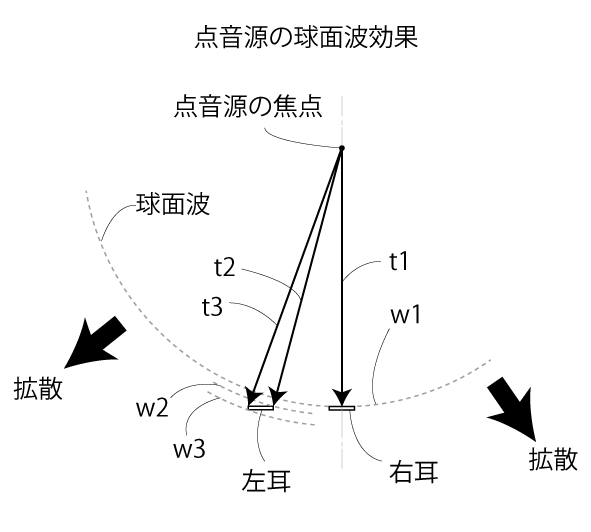
例えば左右の耳の位置が図のように中心からずれている位置にいる時に点音源から拡散波である球面波が拡散する場合、最初にt1の方向へw1の波が右耳へ到達します。この時右耳の全面にほぼ瞬時に波は伝わります。続いてt2の方向へw1の波はw2として左耳の右端へ到達し、続いてt3の方向にw2の波がw3として左耳の左端へ到達します。すなわちこのような特別な配置に限らず、どの様な位置で聞いたとしても、音源に近い方の耳へくる音より、遠い方の耳にくる音の方が、音の滞在する時間が長くなり、右と左の耳では同じ音が複雑にズレています。

このような音の性質を球面波効果、完全な球形でなくても一様に拡散する場合には同様の事になるので、拡散波効果とします。

形体によっては音源の大きさと焦点の大きさとが異なる場合もありますが、球面波効果があるのは焦点の大きさが点の大きさの場合であり、振動板が平行往復運動して音を出す場合は振動板の大きさが焦点の大きさとなり、球面波効果は望めません。

この位相のズレをマイクでは反応できませんが人の耳は外耳の音の反射を利用して片耳でも方向を聞き分けられるようですから、球面波効果を聞き分けられるのは十分可能でしょうし、このような機能が耳にあるからこそ私たちは音を立体に感じられているのでしょう。

このように、振動板から直接拡散波を出すスピーカーで再生すれば片チャンネルでも立体的に聞こえる音で再生することができ、これこそが理想的なスピーカーである事を再確認できます。

,

r

タワミ振動は点音源振動
〜 自然な音を出せる最も有効な方法

では、拡散波の音を出すのにはどのような構造のスピーカーが必要なのかを考えてみます。

もし点音源が現実にあるとしたらそれは球の伸縮振動であり、表面はタワミ振動しています。ならば、同じ様なタワミ振動で、点音源を実現出来るであろう事を確認してみます。

靴音、机を叩いたときの音、ピアノの音、コントラバスの音、などから音が出るのは、床、机、ピアノの響板、コントラバスの本体、などの物体になんらかの力が加わり発生したタワミ振動が空気中に伝わるからです。
この様なタワミ振動とは点音源が振動しているのと同じ事だと理解できます。+

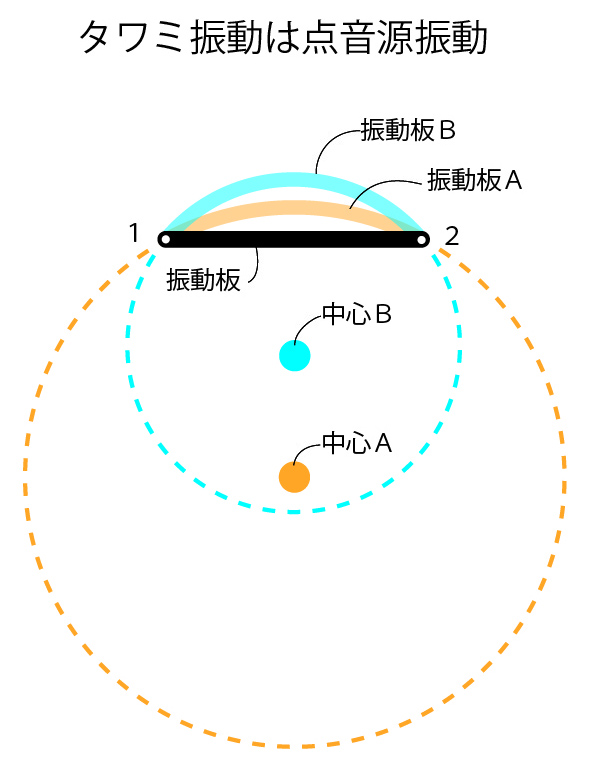
図のモデルにおいて振動板は１と２の位置で固定されている時になんらかの力が加わり振動板が伸びて振動板Aまでタワむとします。この時に振動板は１と２で固定されているので、振動板Aは中心Aの円弧（球の一部の事もある）となります。続いて振動板は伸び続けて振動板Bまでタワむとします。この時振動板Bは中心Bとする円弧となります。つまり、振動板がタワむ振動は中心の位置が振動する円弧の事となります。

すなわち、例えば振動板が１と２で固定されていない場合でも、なんらかの関係で円が正円にならなかったとしても、たとえどんな複雑なタワミ振動だとしても、タワミ振動とは中心の位置が振動する円弧，あるいは円弧の組み合わせとみなす事ができます。この後、振動板が下へタワんだとしても同じように中心の位置が振動する事に変わりはありません。

円弧とはすなわち拡散波である球面波を出す点音源の音源、中心とは大きさゼロの焦点の事なので、タワミ振動は焦点が振動する点音源、タワミ振動は点音源振動と理解でき、球面波効果、拡散波効果も期待できます。

ただし振動板の後ろ方向へも音は出るので、正確に言えば前へ出る正相の半球面波と、後ろへ出る逆相の半球面波，あるいは言葉としてまとめて言えば拡散波となります。

すなわち、理想的なスピーカーである点音源を実現するには、振動板の平行往復運動ではなくてタワミ振動を利用すれば可能となるのです。ですからタワミ振動からは拡散波である球面波の自然の音がするわけです、、、？

一寸待って下さい、という説明をしてきたのですが、実はタワミ振動とは最初から最も自然な音が出せる方法なのでしたね。何故だかわかりますか？その理由は自然界にある物体から音が出るときは，ほとんどタワミ振動で音が出ているからです。

もともとタワミ振動とは、自然な音を出せる最も有効な方法であると、自然の摂理は教えているのでした。

,

r